Insight #7: alles weten over Excel-kwartielen?

Samenvatting:
(1) hoe je met een formule handmatig kwartielen berekent
(2) wat in Excel .INC en .EXC betekenen
(3) duidelijk voorbeeld

Als data analist of scientist raak je nooit uitgeleerd. Zo “herontdekte” ik onlangs sinds de middelbare school weer de betekenis van kwartielen, decielen en percentielen. In Excel kun je ze snel uitrekenen. Vroeger zou dat voldoende zijn maar ik wilde nu eens weten hoe je ze precies en handmatig berekent.

Blind vertrouwen op Excel heeft zo zijn voordelen. Je bespaart veel tijd met het uitzoeken en je zit meestal meteen goed. Maar soms wil je net iets anders dan dat Excel genereert of je twijfelt welke Excel-instelling je moet kiezen. En dan moet je op onderzoek wat ik deed voor kwartielen en decielen in Excel.

Wat zijn kwartielen, decielen en percentielen?

Deze meetwaarden geven je antwoord op vragen zoals hoeveel 10% van mijn beste klanten omzetten. Of wat leveren 20% van je beste aandelen in je beleggingsportefeuille op.

Bij kwartielen deel je je bestand op in 4 groepen (de 25% beste klanten, de 50% beste klanten, de 75% beste klanten of omgekeerd de minst goede klanten). Zet je bij kwartielen vier stappen van 25%, bij decielen zet je tien stappen van 10% en bij percentielen honderd stappen van een procent.

Wat meer formeel . . . volgens WikiPedia is een kwartiel “een . . . geordende set data, de steekproef of populatie, in vier (zo goed mogelijk) gelijke delen opdeelt. Elk deel is in dat geval een kwart van de dataset. Men spreekt van eerste, tweede en derde kwartiel”.

Het handige van kwartielen berekenen in Excel is dat het nagenoeg vanzelf gaat. Een reeks getallen wordt door Excel automatisch gesorteerd en met een parameter geeft je aan welk kwartiel (of deciel of percentiel) moet worden berekend. Daar zijn op YouTube veel instructievideo’s van. Zie onderaan dit blog.

Om goed te begrijpen wat er gebeurt is het interessant om eens uit te pluizen hoe je kwartielen precies berekent en welke “problemen” je zoal tegenkomt.

Kwartielen berekenen . . . een voorbeeld

Stel je belegt in 10 aandelen en die hebben het afgelopen jaar het volgende rendement behaald:
Aandeel AAA gaf een rendement van 28%, aandeel BBB leverde 20% op etc.

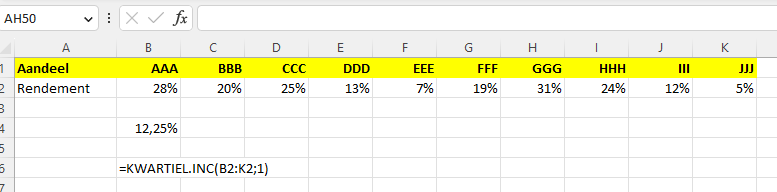
Je ziet dat niet alle je beleggingen evengoed renderen. Dus daarom wil je bijvoorbeeld een kwart van je aandelen vervangen door betere aandelen. Maar welke aandelen zijn dit nu precies die je vervangt? Dat is met bovenstaande tien aandelen al lastig te zien. Laat staan wanneer er 40 aandelen in je portefeuille zitten. Dan kun je gaan sorteren in Excel en zelf wat grenzen bepalen. Maar dat is uiteindelijk veel werk en telkens weer. Bovendien . . . . grote kans dat je Excel-fouten maakt.

In de screenshot staat al de Excel-formule. De cellenrij B2:K2 spreekt voor zich. De parameter “1” geeft aan dat de wilt weten welke 25% van je aandelen het slechts presteren. De uitkomst van de formule is “12,25%” wat wil zeggen dat alle aandelen die minder dan 12,25% renderen een kwart van je aandelenportefeuille uitmaken. In dit geval zijn dat dus de aandelen “JJJ”, “III” en “EEE”

Je zult misschien zeggen “als je 10 aandelen hebt dan is een kwart van die aandelen toch 2,5?” Dat is helemaal waar maar een half aandeel of een halve klant bestaan niet. Maar gegeven deze voorbeeldsituatie wordt er naar boven afgerond. Dat kun je wat makkelijker inzien als je de rendementen van je aandelen sorteer. Er zijn maar drie aandelen die minder dan 12,25% renderen:

Hoe wordt die 12,25% nu precies berekend? Of anders geformuleerd “waar trek je de grens?” want die 12,25% staat nergens. We zijn op zoek naar de aandelen die tot het eerste kwartiel behoren en die kun je met de onderstaande formule bereken.

De formule . . .

Eerst ga je op zoek naar de rank (rangorde):

Rank = K *(N-1)+1
K = het gewenste kwartiel (1e kwartiel = 0,25, 2e kwartiel = 0,5 en het 3e kwartiel = 0,75)
N = aantal elementen van de reeks (in ons geval 10)

Als je de waarden voor het eerste kwartiel in de formule invoert:
Rank = 0,25 * (10 – 1) + 1 = = > 0,25 * 9 + 1 = 3,25

Het eerste kwartiel loopt daarmee 3,25e rangnummer. Het eerste kwartiel bestrijkt dus het gebied van 0 tot 3,25. Oftewel loopt tot ergens tussen het derde en het vierde element resp. de 12% en 13%.

Omdat de rank van het eerste kwartiel 3,25 geen geheel getal is, neem je het derde element uit de reeks (= 12%) en je telt daar een 0,25 keer het verschil tussen de derde en vierde term (13% -/- 12%) bij op. De grenswaarde van het 1e kwartiel wordt dan:

Grenswaarde = 12 + 0,25*(13-12) = = > 12 + 0,25*1 = 12,25 !!!

Bovenstaande berekeningen en sorteringen voert Excel voor jou in de achtergrond uit. Maar je hebt nu inzicht hoe Excel aan de uitkomst komt.

Nu je de formule kent, kun je ook uitrekenen waar voor het 3e kwartiel de grens ligt:

Rank 3e kwartiel = 0,75 * (10 – 1) + 1 = = > 0,75 * 9 + 1 = 7,75

De grenswaarde voor het 3e kwartiel is nu: 24 + 0,75 (25 – 24) = = > 24 + 0,75 * 1 = 24,75
Oftewel, de aandelen HHH, AAA en GGG vormen het 3e kwartiel want zij renderen beter dan 24,75%.

Het 2e kwartiel is altijd gelijk aan de mediaan (= middelste waarde in een reeks). Als de lengte van een reeks oneven is, is de het 2e kwartiel (of mediaan) makkelijk te bepalen. Stel je cijferreeks bestaat uit vijf waarden dan is de middelste waarde (= 3e getal) de grenswaarde van het 2e kwartiel. Bijvoorbeeld de cijferreeks 2, 4, 7, 11 en 12. Dan is het getal “11” de mediaan. Zorg wel dat je de cijferreeks hebt gesorteerd.

Bestaat de cijferreeks zoals in bovenstaand voorbeeld uit 10 waarden (dus even!!!) dan is er geen middelste waarde. Die moet je berekenen en ligt tussen het 5e en 6e element (dus tussen de 19% en 20%).

De uitkomst kun je met blote oog zien en is 19,5% . . . en dat kun je controleren met de besproken formule:

Rank 2e kwartiel = 0,5 * (10 – 1) + 1 = = > 0,5 * 11 = 5,5

Grenswaarde 2e kwartiel = 19 + 0,5* (20 -19) = = > 19 + 0,5 * 1 = 19,5

TIP: check het zelf ook in Excel !!!!

LET OP met Excel . . .

Excel geeft drie mogelijkheden om kwartielen te berekenen (zie screenshot):

EXC = exclusief (je abstraheert van de mediaan)
INC = inclusief (de mediaan wordt in de berekening wel meegenomen)
NB: de ene of de andere methode is theoretisch om het even. Excel, R en Python gebruiken de INC-methode en de TI 84 calculator gaat uit van EXC. Per saldo maakt het niet heel veel verschil. Zie https://www.statology.org/quartile-exc-vs-quartile-inc-excel/ voor een verdieping.

In de praktijk wordt de INC-methode het meest gebruikt.

Ben je toch geinteresseerd in de EXC-berekening dan neem je deze formule om de Rank te bepalen:

Bij EXC . . . Rank = K * (N + 1) = = > 0,25 * (10 + 1) = 2,75
De berekening gaat verder zoals hierboven:

Grenswaarde = 7 + 0,25 * (12% – 7%) = = > 7 + 0,25 * 5 = 10,75

Er is ook nog de “kale” KWARTIEL optie. Deze komt overeen met de INC methode maar wordt door Excel/Microsoft op termijn uitgefaseerd (je ziet dat aan het gele waarschuwingsbord in de screenshot).

Voor decielen en percentielen gaat de berekening min of meer hetzelfde. Als factor in Excel gebruik je voor 0,25 als je het eerste kwartiel via het percentielcommando wilt berekenen. Bij decentielen maakt je in Excel ook gebruik van het commando percentiel (zie bron (7)onderaan dit blog).

Bronnen:
(1) Kwartielen en boxplot
(2) quartile.INC en quartile.EXC in Excel
(3) calculator: calculate quartiles
(4) Quantile (Quartile, Decile and Percentile): Manual Calculation + Microsoft Excel
(5) How to calculate quartiles in Excel
(6) Kwartielen wikipedia NL
(7) Calculate deciles in Excel
(8) Verdieping voor INC en EXC